#matematykaboners #matma #zespolone #liczby #matematyka
Wszystko
Wszystkie
Archiwum
Czy rozumie ktoś potęgowanie liczby rzeczywistych i chciałby pokazać gdzie zrobiłem błąd? Będę wielbił do końca życia (jutro kolos)
#matematykaboners #matma #zespolone #liczby #matematyka
#matematykaboners #matma #zespolone #liczby #matematyka
- 1
@deryt: Zapomniałeś o drugim pierwiastku, tj. o (-1-i) * sqrt(2)/2
@Pavello: Mi się wygodnie się na to patrzy wizualizując sobie to na płaszczyźnie zespolonej. Wiadomo, że podnoszenie liczby zespolonej do kwadratu podwaja jej kąt a moduł się podnosi do kwadratu. W związku z tym wiadomo, że szukając pierwiastka z i (moduł 1 i kąt 90 stopni) będziemy chcieli czegoś, co będzie miało moduł jeden i kąt 45 stopni albo 225
@Pavello: Mi się wygodnie się na to patrzy wizualizując sobie to na płaszczyźnie zespolonej. Wiadomo, że podnoszenie liczby zespolonej do kwadratu podwaja jej kąt a moduł się podnosi do kwadratu. W związku z tym wiadomo, że szukając pierwiastka z i (moduł 1 i kąt 90 stopni) będziemy chcieli czegoś, co będzie miało moduł jeden i kąt 45 stopni albo 225
3
Liczby zespolone
Liczby zespolone odgrywają bardzo ważną rolę zarówno w samej matematyce jak i w technice. Materiał zawiera najważniejsze informacje o liczbach zespolonych, w tym wiele przykładów.
z- 1
- #
- #
- #
- #
- #
- #
Czy taki wzór istnieje? #zespolone #matematyka
@hurtwish: to nieprawda, musisz jeszcze podzielić przez ||z2||^2. Taki wzór powstaje przez pomnożenie licznika i mianownika pierwszego ułamka przez sprzężenie z2 i skorzystanie ze wzoru, że iloczyn liczby i jej sprzężenia to kwadrat modułu.
@Conflagration: To jest dokładnie takie mnożenie (zakładając że przez "dzielnik" miałeś na myśli ułamek). Tyle że da się jeszcze uprościć wynik :)
gdzie przez z' oznaczyłem sprzężenie z.
z1/z2 * z2'/z2' = (z1 * z2') / (z2 * z2') = (z1 * z2') / ||z2||^2 gdzie przez z' oznaczyłem sprzężenie z.
- 2
Każdy z wykładowców ma inne słówko na określenie części urojonej, imaginalis, imaginarium, imaginatis, immaterialis.
No #!$%@? zdecydujta się, panowie doktorowie inżynierzy rehabilitowani magistry, job jego mać.
#goszkiezale #studbaza #zespolone
No #!$%@? zdecydujta się, panowie doktorowie inżynierzy rehabilitowani magistry, job jego mać.
#goszkiezale #studbaza #zespolone
28
Jak są definiowane potęgi liczb zespolonych?

Moje tłumaczenie specjalnie z myślą o jajogłowych z Wykopu. Jeżeli wpis okaże się interesujący to zacznę pisać częściej, jednak będą to już teksty "własnej produkcji".
z- 5
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
42
Luzacki kurs liczb zespolonych. Czyli jak tu nie kochać matematyki.
Z racji braku wiadomości o liczbach zespolonych, zacząłem szukać pomocy w internecie. Oto kurs od luźniejszego "wykładowcy" dla luźniejszego studenta ;). Na początek polecam przedostatni akapit pierwszej strony.
z- 12
- #
- #
- #
- #
- #
- #
7
Kierki zespolone...
Ciekawy wariant gry w kierki (wersji amerykańskiej, nie naszej) dla osób o skrzywieniu matematycznym
z- 1
- #
- #
- #
- #
- #
- #
- #
- #



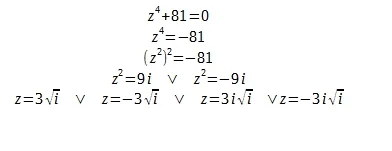





(zapis... Wiem taki sobie, ale chodzi mi tylko o sam wynik) #matematyka #zespolone
źródło: comment_FSDaef0OWV24rxe60BUuL9prcflMeOlP.jpg
Pobierz